In this post, I will talk about a common approach for generating all permutations, its complexity, and how big the argument list can be that makes the stack overflow using OCaml. I borrow some pictures and work from typeocaml.
The insert-into-all-positions solution
Let’s assume that we have a set of all permutations for a set of 3 elements. Thus totally
there are 6 permutations. For example, let 3 elements be [1;2;3], then 6 permutations
are [1;2;3], [2;1;3], [2;3;1], [1;3;2], [3;1;2], and [3;2;1].
So now what if we put a new element, say 4, into the set of 4 elements [1;2;3;4]? What
we need to do is combining the new element 4 into the previous set of permutations to
generate a new set of permutations.
Let’s see how a new element is inserted into a permutation. Consider a permutation of 3
elements [1;2;3], there are 4 possible positions (before 1, 2, 3, and after 3)
to insert 4 as shown in the figure.
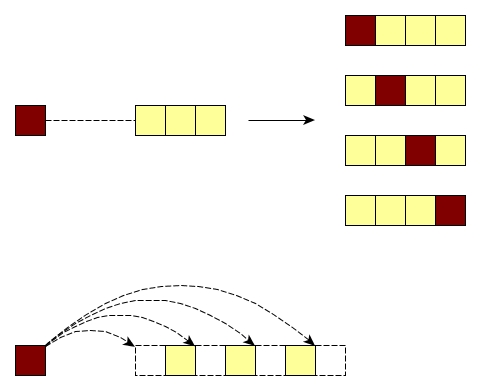
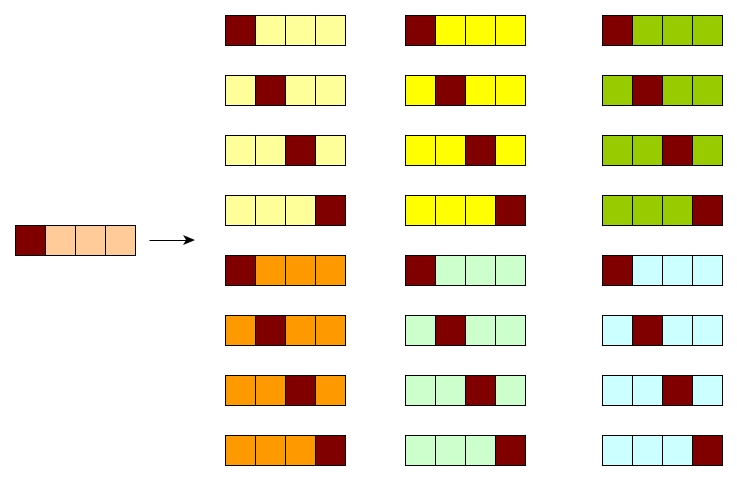
Therefore, with 6 previous permutations we have totally \(4 * 6 = 24\) new permutations
if we insert the new element 4.
Code
The implementation can be done by the following two functions. The insert_all_positions
function inserts a new element given a set of permutations. The permutations function
recursively generates all permuations. If the number of elements is 0 or 1, then there
is only 1 permutation. Here is the Gist.
let insert_all_positions x l =
let rec aux prev acc l =
match l with
| [] -> (prev @ [x]) :: acc |> List.rev
| hd::tl as l -> aux (prev @ [hd]) ((prev @ [x] @ l) :: acc) tl
in aux [] [] l;;
let rec permutation l =
match l with
| [] -> []
| hd::[] -> [[hd]]
| hd::tl -> List.fold_left (fun acc p -> acc @ insert_all_positions hd p) [] (permutation tl);;
Complexity
The complexity depends on the number of permuations which is \(n!\)
(n is the number of elements). Assume that the complexity of insert a new element to
a permuation takes 1 time unit, thus for a permuation consisting of m elements, it
takes \((m + 1)\) time units. Therefore for each recursive call, we have the complexity
\(T(m) = m * T(m - 1)\). The complexity of the algorithm should be
\(T(n) = n * T(n - 1)\) \(= n * (n - 1) * T(n - 2)\) \(= ...\) \(= n * (n-1) * (n - 2) * ... * 2 * T(1) = n!\)
Stack overflow
When I run the code above with OCaml version 4.02.1, stack overflow occurs likely with the number of elements is 9. For example,
permutation [1;2;3;4;5;6;7;8;9];;
Stack overflow during evaluation (looping recursion?).
Dynamic permutations
One interesting way to deal with big number of elements is generating one permutation at each time. One can employ the Johnson Trotter algorithm to generate a different permutation each time. I will talk about this algorithm in a next post.
