In the previous post, I talked about heap data structure, a tree-based implementation in OCaml. This post will discuss how it is used to implement the heap sort algorithm. This sorting algorithm has \(O(nlogn)\) worst-case time complexity.
Algorithm
Assume that we want to sort the list [4; 1; 5; 3; 2] in decreasing order. We assume further that the input list is represented by a complete binary min heap with 5 nodes as shown on the top of Figure 1.
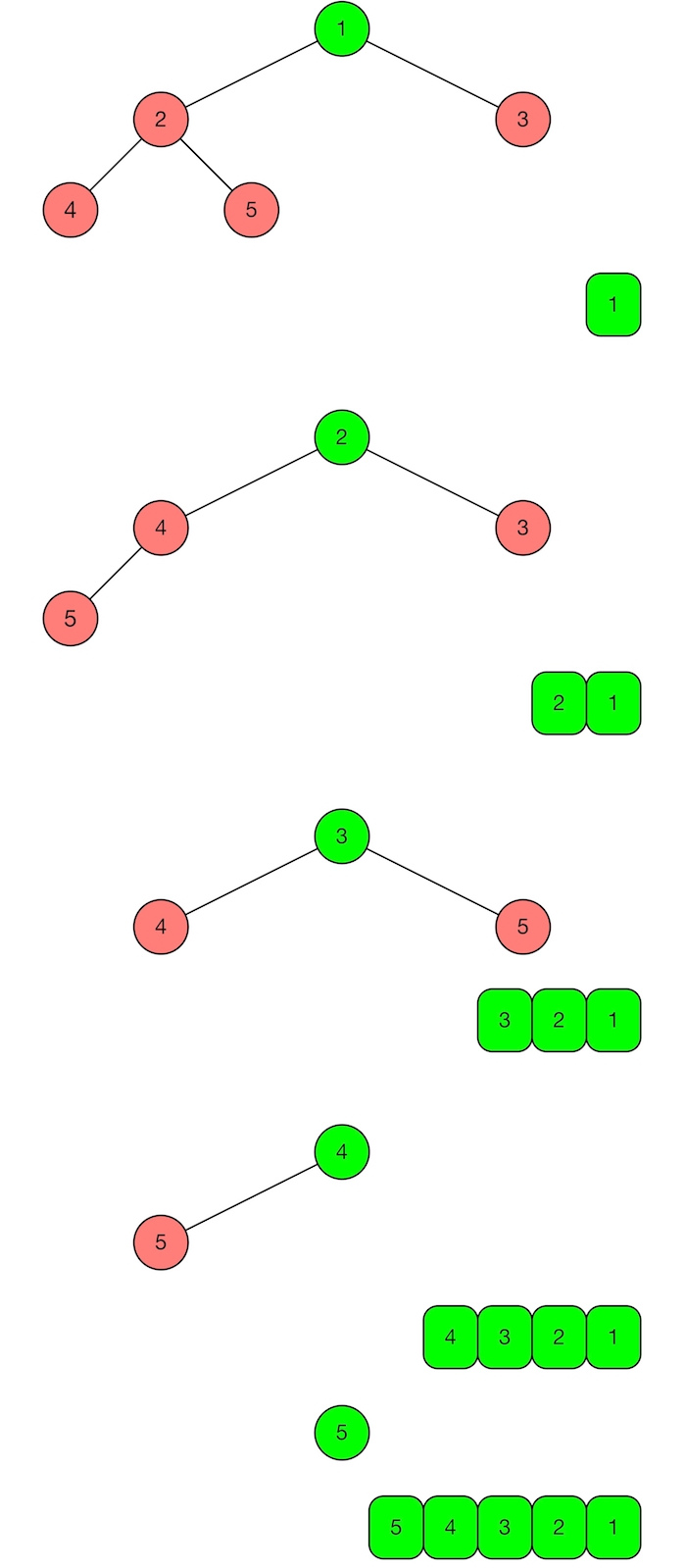
To sort the list we create an empty list as the output list. We pick the key value 1 of the heap’s root and put it into the output list. Then we remove the root Node 1 from the heap. After these actions, we get a new heap with the root is Node 2 and a new output list with one element 1. If we do the actions above until the heap is empty (e.g., represented by a node Leaf), then we get the final output list is in decreasing order [5; 4; 3; 2; 1]. The process is depicted in Figure 1. Thus the heap-sort algorithm can be divided into the following steps. The result list is initialized empty.
- Build a complete binary min heap from the input list
- Get the root of the heap and concatenate it with the result list
- Remove the root. If the heap is not empty, then goto step 2
- If the sorting direction is decreasing then return the result list, otherwise, return the reversed list
The heap building is \(O(nlogn)\) time complexity. The getting and removing the root operations are \(O(1)\) and \(O(logn)\), respectively, and they are called \(n\) times. Therefore, the time complexity of the heap-sort algorithm is \(O(nlogn)\).
Code
This post demonstrates the use of extending modules with functor in OCaml programming language as well.
Let’s see how this works in the context of the Heap module to add the additional functionality
for sorting. Instead of writing a heap-sort module extending the heap module with the sorting function by hand, we use a functor to add this functionality to the heap module that supports the fold_on_min function.
We create a new module Heapsort that automates the process of adding sorting function to the Heap module. As you can see, Heapsort contains a type k of the Heap key type, a function sort_list to sort a list of this type, and a functor Make that allows one to extend a Heap module.
(************************************)
(* Heap-sort *)
(* Van Chan Ngo *)
(************************************)
(** Implementation of binary heap over ordered types *)
open Heap
type direction = Dec | Inc
module type Heapsort = sig
type k
val sort_list : direction -> k list -> k list
end
module Make (H : Heap) : (Heapsort with type k = H.key)
open Heap
type direction = Dec | Inc
module type Heapsort = sig
type k
val sort_list : direction -> k list -> k list
end
module Make (H : Heap) = struct
type k = H.key
let sort_list d l =
let h = H.of_list l in
let ol = H.fold_on_min (fun a k -> k::a) [] h in
match d with
| Dec -> ol
| Inc -> List.rev ol
end
In order to apply the functor, we create a heap module from a module OrdertedType. For example, I want to sort a list of integer pairs, I first create a module IntPair module. Then a heap module H is created from IntPair. Finally, a heap-sort module is created from H using the functor.
open Heap
open Heapsort
module IntPair =
struct
type t = int * int
let to_string x =
let (x1,x2) = x in
"(" ^ (string_of_int x1) ^ "," ^ (string_of_int x2) ^ ")"
let compare (x1,y1) (x2,y2) =
if x1 > x2 then
Gt
else if x1 < x2 then
Lt
else
begin
if y1 > y2 then
Gt
else if y1 < y2 then
Lt
else
Eq
end
end
module H = Heap.Make(IntPair)
module HS = Heapsort.Make(H)
let _ =
let ol = HS.sort_list (Inc :direction) [(1,2); (2,3); (2,343223); (432332525,1333); (342395835289,29235899589); (248,35989835)] in
List.iter (fun (x,y) -> Printf.printf "(%d,%d) " x y) ol; Printf.printf "\n"
The sorted output list is
(1,2) (2,3) (2,343223) (248,35989835) (432332525,1333) (342395835289,29235899589)
