In this post, I will talk about the heap data structure, a specialized tree-based data structure. I will recall how it can be implemented in imperative languages. Finally, I will discuss how heap can be implemented with lists in functional languages and show that it does not satisfy the requirements. A tree-based implementation in OCaml will also be given in this post.
Heap data-type
A (complete) binary (min) heap is a binary tree that satisfies the following conditions:
-
Shape property: it is a complete binary tree; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
-
Heap property: the key stored in each node is less than or equal to the keys in the node’s children, according to some total order.
Figure 1 shows an example of a complete binary min heap, the numbers represent the value of the keys in the nodes.
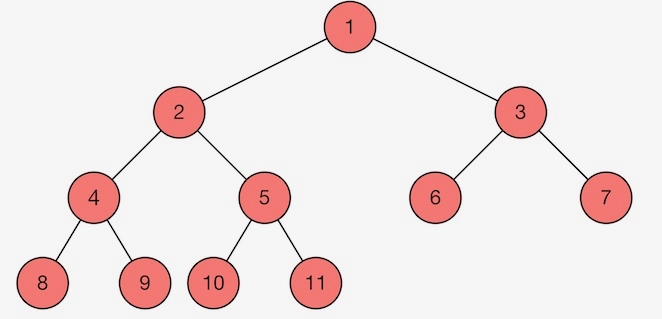
Heap is known for its efficient algorithms (logarithmic time complexity) of inserting and deleting the smallest element in implementing a priority queue. It is also used in implementing heapsort algoritm that has \(O(nlogn)\) time complexity.
In imperative world, a heap is generally placed in an array with the layout of complete
binary tree, mapping complete binary tree nodes to the array indices. For instance, with
the zero-based array, the root node is represented by index 0, if i is the index of
the parent, then the indices of its left and right child are: left_child(i) = 2*i + 1
and right_child(i) = 2*i + 2. However, in functional languages, if we implement an array
using list data-structure. Then we cannot obtain the constant time complexity for
accessing elements of the array. Therefore, lists cannot be used to implement efficient
heaps. Instead, we need to use tree data structures to implement heaps in functional world.
The following will explain how we heaps are implemented in this way, especially how a new
node is inserted into and the min node is removed from a heap with \(O(logn)\) time
complexity.
A complete binary heap is represented by a complete binary tree that satisfies the heap
property. A node can be a terminal node, called Leaf or a non-terminal node, called
Node, that contains
information about the number of nodes, the height, the key, its left and right trees.
We will see that the number of nodes and the height help us decide to add a new node on
the left or right child tree. The heap data-type is given in the following snippet.
(** type of node value. *)
type key = El.t
(** a node contains # nodes, height, left tree, key, and right tree. *)
type heap = Leaf
| Node of int * int * heap * key * heap
Insert a new node
We consider an example of inserting 0 into the following integer heap. We first need to determine which direction for inserting, insert to the left subtree or to the right subtree, in order to satisfy the shape property. In this example, the left tree is full, so we should insert 0 into the right tree. We insert 0 to the bottom level of the heap. Because 0 is smaller than its parent, 6, so we swap 0 and 6. After swapping, it is obvious that 0 is smaller than 3, thus we swap again 0 and 3. Finally, 0 is smaller than 1, so we swap 0 and 1. At this point, the new heap satisfies both shape property and heap property.
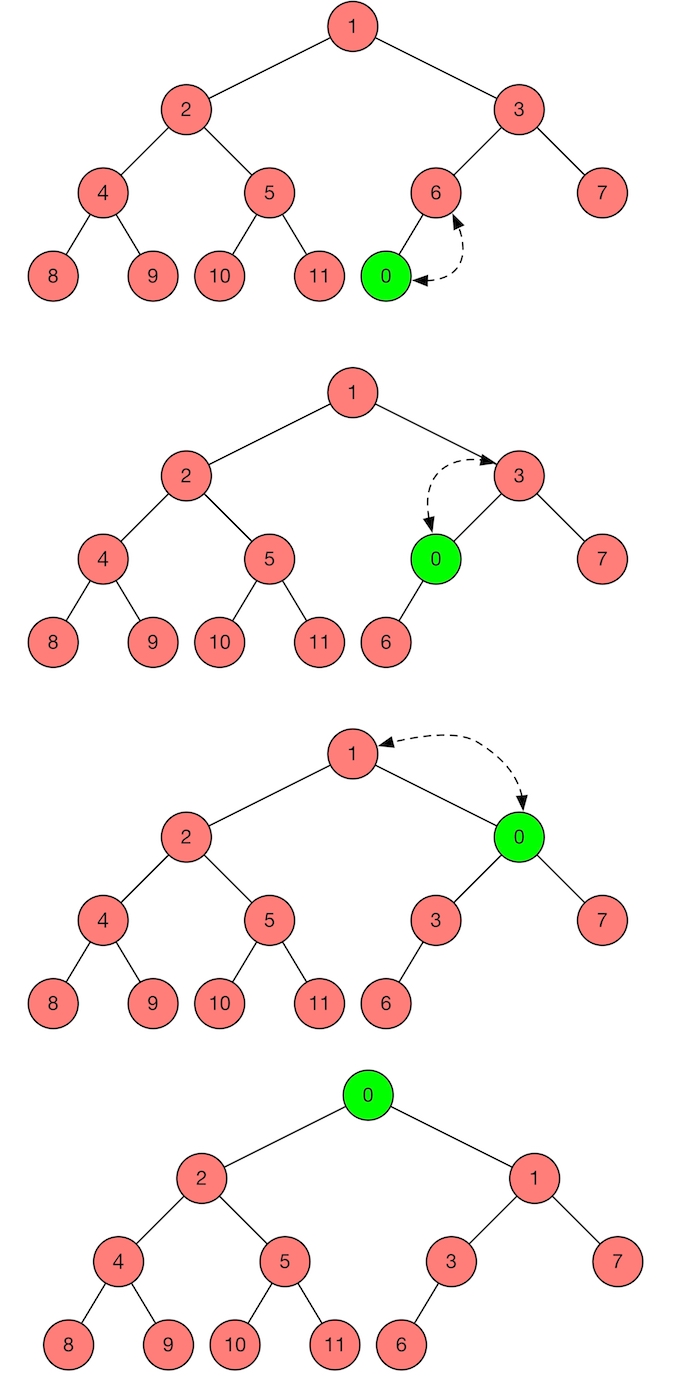
In general, we have the following algorithm that takes \(O(logn)\) runtime to insert a key into a heap.
-
Since \(2^h <= n <= 2^{h+1} - 1\), if \(n = 2^{h+1} - 1\) (the tree is perfect complete) then insert to the left tree. Or if \(2^h <= n < 2^h + 2^{h-1}\) (the left tree is not full) then insert to the left tree. Otherwise insert to the right tree
-
Add the new key to the bottom level of the heap
-
Compare the added key with its parent, if they are in the correct order, then stop
-
If not, swap it with its parent, then goto 3.
Remove the min node
Assume that we want to remove the root of the following heap. We first replace the root with the last node on the bottom of the heap, meaning that the new root is now 11. We then compare 11 with its children in order to make the heap property satisfied. Because 11 is bigger than the smallest child 2, so we swap them. After that, 11 is bigger than the smallest child 4, we swap them again. Now, 11 is bigger than the smallest child 8, we finally swap them. At the end, we have a new heap that satisfies all conditions, namely shapre property and heap property.
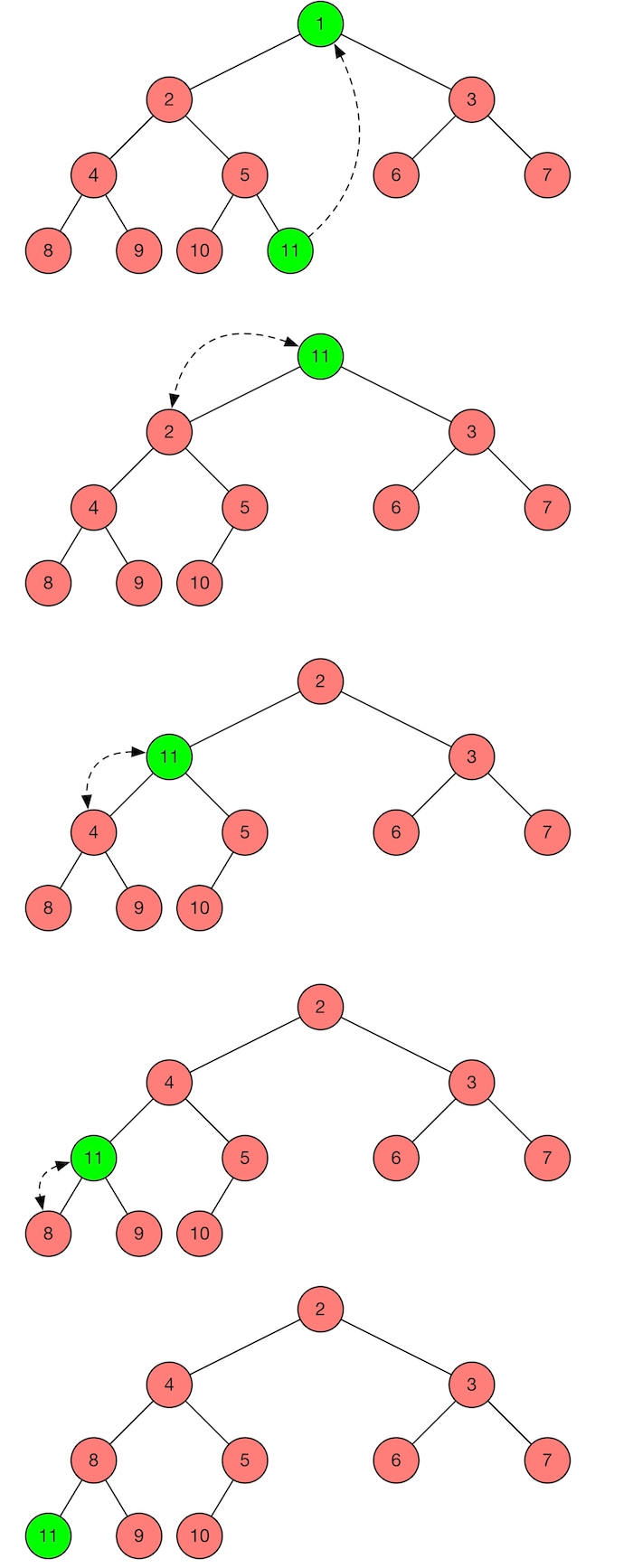
The \(O(logn)\) time complexity algorithm of removing the root from the heap is given as follows.
-
Replace the root with the last node on the last level of the heap
-
Compare the new root with its children, if they are in the correct order, then stop
-
If not, swap the root with the smallest child, then goto 2
Implementation
The full implementation is given below, in which many other utility functions for heap manipulation are provided.
(************************************)
(* Heap *)
(* Van Chan Ngo *)
(************************************)
(** Implementation of binary heap over ordered types *)
type order = Lt
| Eq
| Gt
module type OrderedType =
sig
(** the type of the keys. *)
type t
val compare : t -> t -> order
val to_string : t -> string
end
module type Heap =
sig
(** the type of the elements. *)
type key
(** the type of a heap. *)
type heap
(** create an empty heap. *)
val create : unit -> heap
(** check a heap is empty. *)
val is_empty : heap -> bool
(** return the size of the heap. *)
val size : heap -> int
(** return the height. *)
val height : heap -> int
(** insert a new key. *)
val insert : key -> heap -> heap
(** remove the last node. *)
val remove_last_node : heap -> heap
(** delete the root. *)
val remove_min : heap -> heap
(** get the root. *)
val get_min : heap -> key
(** create a heap from list. *)
val of_list : key list -> heap
(** heap fold. *)
val fold_on_min : ('a -> key -> 'a) -> 'a -> heap -> 'a
val fold_pre_order : ('a -> key -> 'a) -> 'a -> heap -> 'a
(** merge two heaps into one valid heap. *)
val merge : heap -> heap -> heap
(** search a key. *)
val search : key -> heap -> bool
(** to string in pre-order. *)
val to_string : heap -> string
end
module Int : OrderedType with type t = int
module Make (El : OrderedType) : Heap with type key = El.t
type order = Lt | Eq | Gt
module type OrderedType =
sig
(** the type of the keys. *)
type t
val compare : t -> t -> order
val to_string : t -> string
end
module type Heap =
sig
(** the type of the elements. *)
type key
(** the type of a heap. *)
type heap
(** create an empty heap. *)
val create : unit -> heap
(** check a heap is empty. *)
val is_empty : heap -> bool
(** return the size of the heap. *)
val size : heap -> int
(** return the height. *)
val height : heap -> int
(** insert a new key. *)
val insert : key -> heap -> heap
(** remove the last node. *)
val remove_last_node : heap -> heap
(** delete the root. *)
val remove_min : heap -> heap
(** get the root. *)
val get_min : heap -> key
(** creat a heap from list. *)
val of_list : key list -> heap
(** heap fold. *)
val fold_on_min : ('a -> key -> 'a) -> 'a -> heap -> 'a
val fold_pre_order : ('a -> key -> 'a) -> 'a -> heap -> 'a
(** merge two heaps into one valid heap. *)
val merge : heap -> heap -> heap
(** search a key. *)
val search : key -> heap -> bool
(** to string in pre-order. *)
val to_string : heap -> string
end
module Int =
struct
type t = int
let to_string x = string_of_int x
let compare x y =
if x > y then
Gt
else if x < y then
Lt
else
Eq
end
module Make (El : OrderedType) =
struct
type key = El.t
(** a node contains # nodes, height, left tree, key, and right tree. *)
type heap = Leaf
| Node of int * int * heap * El.t * heap
let create () =
Leaf
let is_empty aheap =
match aheap with
| Leaf -> true
| _ -> false
let size aheap =
match aheap with
| Leaf -> 0
| Node (n, _, _, _, _) -> n
let height aheap =
match aheap with
| Leaf -> 0
| Node (_, h, _, _, _) -> h
(** Insert x into a heap (n, h, tree).
* Since 2^h <= n <= 2^(h+1) - 1,
* if n = 2^(h+1) - 1 (the tree is perfect complete
* then insert to the left tree
* or if 2^h <= n < 2^h + 2^(h-1) (the left tree is
* not full then insert to the left tree
* else insert to the right tree.
*
* 1. Add the new key to the bottom level of the heap
* 2. Compare the added key with its parent,
* if they are in the correct order, then stop
* 3. If not, swap it with its parent, then goto 2.
*)
let insert_to_left n h =
let lb = 1 lsl h in
let up = 1 lsl (h + 1) in
if (n = up - 1) || (n >= lb && n < (lb + lb/2 - 1)) then
true
else
false
let compute_new_height n h =
let up = 1 lsl (h+1) in
if n = up - 1 then
h + 1
else
h
let rec insert x aheap =
match aheap with
| Leaf -> Node (1, 0, Leaf, x, Leaf)
| Node (n, h, l, k, r) ->
let newh = compute_new_height n h in
if insert_to_left n h then
let nlh = insert x l in
begin match nlh with
| Leaf -> Node (n+1, newh, Leaf, k, r)
| Node (ln, lh, ll, lk, lr) as nlh ->
begin match El.compare lk k with
| Lt -> Node (n+1, newh, Node (ln, lh, ll, k, lr), lk, r)
| _ -> Node (n+1, newh, nlh, k, r)
end
end
else
let nrh = insert x r in
begin match nrh with
| Leaf -> Node (n+1, newh, l, k, Leaf)
| Node (rn, rh, rl, rk, rr) as nrh ->
begin match El.compare rk k with
| Lt -> Node (n+1, newh, l, rk, Node (rn, rh, rl, k, rr))
| _ -> Node (n+1, newh, l, k, nrh)
end
end
(** Remove the root from the heap.
* 1. Replace the root with the last node on the last level of the heap
* 2. Compare the new root with its children, it they are in the correct
* order, then stop
* 3. If not, swap the root with the smallest children, then goto 2
*)
let remove_on_left n h =
let lb = 1 lsl h in
if (n >= lb && n <= (lb + lb/2 - 1)) then
true
else
false
let remove_new_height n h =
let lb = 1 lsl h in
if n = lb then
h - 1
else
h
let rec heapify aheap =
match aheap with
| Leaf as ah -> ah
| Node (n, h, l, k, r) as ah ->
begin match (l, r) with
| (Leaf, Leaf) -> ah
| (Leaf, Node (rn, rh, rl, rk, rr)) ->
begin match El.compare rk k with
| Lt ->
Node (n, h, Leaf, rk, Node (rn, rh, rl, k, rr))
| _ -> ah
end
| (Node (ln, lh, ll, lk, lr), Leaf) ->
begin match El.compare lk k with
| Lt ->
Node (n, h, Node (ln, lh, ll, k, lr), lk, Leaf)
| _ -> ah
end
| (Node (ln, lh, ll, lk, lr), Node (rn, rh, rl, rk, rr)) ->
let cp1 = El.compare lk k in
let cp2 = El.compare rk k in
let cp3 = El.compare lk rk in
begin match (cp1,cp2) with
| (Lt, _) | (_, Lt) ->
begin match cp3 with
| Lt ->
Node (n, h, heapify (Node (ln, lh, ll, k, lr)), lk, Node (rn, rh, rl, rk, rr))
| _ ->
Node (n, h, Node (ln, lh, ll, lk, lr), rk, heapify (Node (rn, rh, rl, k, rr)))
end
| (_, _) -> ah
end
end
let rec remove_last_node_aux aheap =
match aheap with
| Leaf -> (None, Leaf)
| Node (1, 0, Leaf, k, Leaf) -> (Some k, Leaf)
| Node (n, h, l, k, r) ->
let newh = remove_new_height n h in
if remove_on_left n h then
let onlh = remove_last_node_aux l in
begin match onlh with
| (None, Leaf) -> (None, Leaf)
| (Some dk, nlh) ->
(Some dk, Node (n-1, newh, nlh, k, r))
| _ -> failwith "Remove_last_node_aux: Invalid heap"
end
else
let onrh = remove_last_node_aux r in
begin match onrh with
| (None, Leaf) -> (None, Leaf)
| (Some dk, nrh) -> (Some dk, Node (n-1, newh, l, k, nrh))
| _ -> failwith "Remove_last_node_aux: Invalid heap"
end
let remove_last_node aheap =
let (_, h) = remove_last_node_aux aheap in
h
let remove_min aheap =
match aheap with
| Leaf -> Leaf
| Node (_, _, Leaf, k, Leaf) -> Leaf
| _ ->
let (ok, nheap) = remove_last_node_aux aheap in
begin match ok with
| None -> nheap
| Some dk -> begin match nheap with
| Node (n, h, l, k, r) -> heapify (Node (n, h, l, dk, r))
| _ -> failwith "Remove_min: Invalid heap"
end
end
let get_min aheap =
match aheap with
| Leaf -> failwith "Heap is empty"
| Node (_, _, _, k, _) -> k
let of_list l =
let h = create () in
List.fold_left (fun ah k -> insert k ah) h l
let rec fold_on_min f a0 aheap =
match aheap with
| Leaf -> a0
| Node (n, h, l, k, r) ->
fold_on_min f (f a0 k) (remove_min aheap)
let rec fold_pre_order f a0 aheap =
match aheap with
| Leaf -> a0
| Node (n, h, l, k, r) ->
let al = fold_pre_order f (f a0 k) l in
fold_pre_order f al r
let merge heap1 heap2 =
match (heap1, heap2) with
| (Leaf, Leaf) -> Leaf
| (_, Leaf) -> heap1
| (Leaf, _) -> heap2
| (_, _) ->
let f ah k =
insert k ah
in
begin match El.compare (get_min heap1) (get_min heap2) with
| Lt ->
fold_pre_order f heap1 heap2
| _ ->
fold_pre_order f heap2 heap1
end
let rec search x aheap =
match aheap with
| Leaf -> false
| Node (_, _, Leaf, k, Leaf) ->
begin match El.compare k x with
| Eq -> true
| _ -> false
end
| Node (_, _, Leaf, k, r) ->
begin match El.compare k x with
| Eq -> true
| _ -> search x r
end
| Node (_, _, l, k, Leaf) ->
begin match El.compare k x with
| Eq -> true
| _ -> search x l
end
| Node (_, _, Node (ln, lh, ll, lk, lr), k, Node (rn, rh, rl, rk, rr)) ->
begin match El.compare k x with
| Eq -> true
| _ -> let cp1 = El.compare x lk in
let cp2 = El.compare x rk in
begin match (cp1, cp2) with
| (Eq, _) -> true
| (Lt, _) -> search x (Node (rn, rh, rl, rk, rr))
| (_, Eq) -> true
| (_, Lt) -> search x (Node (ln, lh, ll, lk, lr))
| (_, _) -> if (search x (Node (ln, lh, ll, lk, lr))) then
true
else search x (Node (rn, rh, rl, rk, rr))
end
end
let to_string aheap =
let f s k = s ^ (El.to_string k)
in
fold_pre_order f "" aheap
end
